Nuevo método para estudiar las leyes de los anillos de los árboles

La revista Scientific Reports ha publicado recientemente un innovador trabajo, del que es coautor el profesor de la Universidad Politécnica de Madrid Juan Carlos Nuño, sobre las leyes que rigen los procesos de crecimiento de interfases en la naturaleza descritas mediante redes complejas.

La investigación —que realizó Nuño, profesor de Matemáticas de la Escuela Técnica Superior de Ingenieros de Montes, junto a Antonio Brú y Manuel Fernández, de la Universidad Complutense de Madrid, y Elisa Alós, de la Universidad Pompeu Fabra de Barcelona— supone una profunda innovación en el conocimiento de las propiedades dinámicas de las interfases utilizando la teoría de redes complejas aplicadas a campos como las ciencias biológicas o sociales.

Según explica la nota de prensa de la UPM, recogida por el Instituto de la Ingeniería de España, muchos sistemas reales y diferentes fenómenos físicos se han descrito con éxito al considerarlos como redes complejas compuestas por gran número de elementos que interactúan. En esta larga lista podemos encontrar, por ejemplo, los sistemas biológicos y químicos, las redes neuronales, el metabolismo celular o las especies que interactúan, pero también internet y las redes sociales.

Sin embargo, la teoría de las redes complejas no se había aplicado hasta la fecha para describir el crecimiento de los tumores sólidos y el proceso de transformación (interfase) que se desarrolla entre el borde del tejido tumoral y el sano. Ya en trabajos previos del profesor Brú se describía el perímetro de este tipo de tumores como compatible con una dinámica regida por la lucha por el espacio que se genera durante la batalla entre las células cancerígenas y las células sanas.

En opinión de Nuño, el nuevo artículo revela que este descubrimiento, que en su momento dio lugar a cierta polémica, se va a poder corroborar mediante el método que se describe en este estudio.

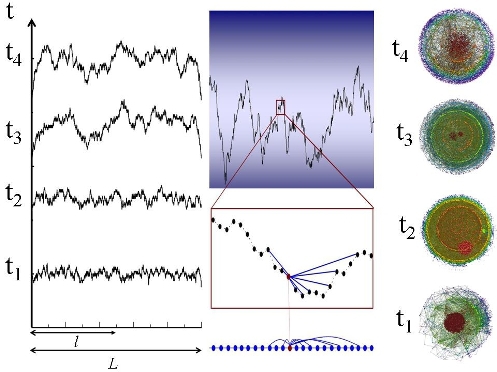
Interfases

La metodología que se presenta en este trabajo abre toda una nueva línea de investigación en el estudio de la dinámica de interfases. Hay que resaltar que las interfases, bordes o fronteras, están presentes en todos los sistemas físicos que presentan dos o más fases.

El algoritmo de visibilidad, que ya se está aplicando con éxito para analizar series temporales, puede aplicarse al estudio de datos espaciales unidimensionales que cambian con el tiempo. Es esta una novedad importante. Además, como comentan los autores del artículo, esta aplicación puede provocar un avance en el conocimiento de las propiedades dinámicas de las redes complejas de enorme importancia en otros campos como las ciencias biológicas y sociales.

Una interfase se puede entender como una curva de separación entre dos estados que se mueve con el tiempo. En la naturaleza encontramos ejemplos que van desde la formación de estructuras moleculares hasta la aparición de frentes invasivos en ecosistemas, pasando por la propagación de fluidos a través de medios porosos, la formación de colonias celulares o tumores y el desarrollo de los anillos de los árboles.

“Por concretar y hacernos una idea, imaginemos un papel de fumar extendido que empieza a consumirse por uno de sus lados. A medida que el tiempo transcurre, se observa una clara separación entre el papel intacto y la parte que se ha ido quemando. La curva teórica que separa ambas partes forma la interfase. La forma de la curva también cambia a medida que se desplaza hacia el otro extremo quemando el papel. La manera en la que se produce este desplazamiento, así como los factores que intervienen en la modificación de la forma de la curva, son objeto de estudio de los físicos, tanto teóricos como experimentales”, explica Nuño.

Esta investigación, basada en los conocimientos obtenidos en los últimos años sobre redes complejas, va a permitir una nueva caracterización de las interfases dinámicas en todos los ámbitos en los que se presenten, asegura el profesor de la UPM. De hecho, según subraya, estos procesos se pueden entender como redes de visibilidad en evolución.

Los autores del trabajo consideran que con esta metodología se puede incluso estudiar la estructura de los anillos de los árboles con el objetivo de describir su formación y relación con las condiciones ambientales y climáticas que soportan. En su opinión, la aplicación del algoritmo de visibilidad a otros procesos físicos espaciales va a permitir clarificar algunas cuestiones de la teoría clásica no resueltas todavía.

Referencia bibliográfica:

A. Brú, E. Alós, J. C. Nuño & M. Fernández de Dios: Scaling in complex systems: a link between the dynamics of networks and growing interfaces. Scientific Reports (2014). DOI:10.1038/srep07550.