
La recolección de comida de muchas especies de hormigas está basada en la comunicación indirecta mediante el uso de feromonas. Durante todo el camino recorrido por una hormiga desde el hormiguero hasta la fuente de comida y viceversa, ésta va depositando feromonas en el suelo formando las denominadas rutas de feromona.
El resto de hormigas pueden percibir estas feromonas y, de hecho, tienden a escoger como recorrido aquellas vías que muestren una mayor concentración de éstas.
En el momento justo en que comienza la recolección de comida, al no haberse puesto aún en movimiento ninguna hormiga, no se ha depositado tampoco feromona alguna, por tanto, las hormigas tenderán a moverse en cualquier dirección.
Algunas hormigas encontrarán, por azar, una fuente de comida y marcarán con feromona la vía que les ha llevado a ella. Esta feromona estimulará a más hormigas a repetir esa vía ya marcada, incrementando así la concentración de feromona.
Cuanto más recta sea una vía, más rápidamente puede ser recorrida, y por tanto mayor incremento de feromona recibirá por unidad de tiempo. De este modo, las hormigas convergen hacia una línea -casi- recta que une el hormiguero y la fuente de comida.
Feromonas y hormigas artificiales
Este modelo de comportamiento le sirvió al investigador italiano Marco Dorigo como base para el desarrollo de algoritmos bio-inspirados, denominados algoritmos de hormigas.
Éstos se aplican para problemas de optimización combinatoria, donde el objetivo es ordenar de manera óptima una secuencia de valores discretos.
Mediante el uso de una tabla de feromona artificial se organiza a una colonia de hormigas, también artificiales, para que cooperativamente encuentren una combinación óptima de valores.
Una hormiga artificial construye una secuencia de valores, incrementándose a continuación consecuentemente el nivel de feromona. Ese nivel servirá para restringir la elección del siguiente valor de la secuencia entre aquellos valores concretos presentes en la tabla de feromona así como para indicar la probabilidad de escoger cada uno de dichos valores.
De este modo, cuando una hormiga está buscando su siguiente valor, puede utilizar la tabla para decidir qué valor escoger después del último utilizado.
Si se vincula la cantidad de feromona depositada a la calidad de una solución, cuanto mejor sea una secuencia, mayor incremento de feromona recibirá, y por tanto será más usada.
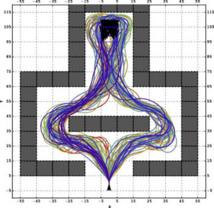
De la ruta de las hormigas a la ruta del barco
Como se puede observar el principio teórico es el mismo, en las hormigas reales se deposita en el suelo una cantidad de feromona que indica qué dirección tomar en cada momento.
Cuanto mayor es la concentración de feromona, mayor es la probabilidad de escoger una dirección determinada.
En las hormigas artificiales, se marca en una tabla de feromona artificial el valor a escoger según el último valor tomado. Y del mismo modo, cuanto mayor sea la marca, más probabilidades habrá de escoger dicho valor.
Un Grupo de investigación Ingeniería de Sistemas, Control, Automática y Robótica (ISCAR) de la Universidad Complutense de Madrid (UCM) se ha basado en los algoritmos de hormigas para optimizar la maniobra de un barco autónomo.
”El problema consiste en obtener una secuencia óptima de velocidad y rumbo que permita trazar una maniobra realizable en el menor tiempo posible”, explica Jose Mª Girón Sierra, profesor del Departamento de Arquitectura de Computadores y Automática y coautor del estudio publicado en la revista Expert Systems with Applications.
Las hormigas comienzan trazando trayectorias al azar. A medida que van alcanzando el objetivo, marcan con la feromona la trayectoria seguida. Así comienzan a aparecer marcas de feromona, marcas que guían la trayectoria para trazar la maniobra.
La cantidad de marca está vinculada al tiempo que tarda el barco en cada trayectoria, por tanto, las trayectorias más cortas recibirán un incremento mayor de feromona. Así, con el tiempo, las trayectorias se van optimizando, hasta que convergen en aquélla que permite trazar la maniobra en el menor tiempo posible.
Referencias bibliográficas:
Escario, J. B., et al. Optimisation of autonomous ship manoeuvres applying Ant Colony Optimisation metaheuristic. Expert Systems with Applications (2012), doi:10.1016/j.eswa.2012.02.069.














Hacer un comentario